Pengertian Matriks
Matriks adalah susunan sekelompok bilangan dalam suatu jajaran
berbentuk persegi panjang yang diatur berdasarkan baris dan kolom dan
diletakkan antara dua tanda kurung. Tanda kurung yang digunakan untuk mengapit
susunan anggota matriks tersebut dapat berupa tanda kurung biasa atau tanda
kurung siku. Setiap bilangan pada matriks disebut elemen (unsur) matriks.
Kumpulan elemen yang tersusun secara horizontal disebut baris, sedangkan
kumpulan elemen yang tersusun secara vertikal disebut kolom. Suatu matriks yang memiliki m baris dan n kolom disebut
matriks m x n dan disebut
sebagai matriks yang memiliki orde m x n. Penulisan matriks menggunakan huruf kapital dan tebal.
Pembahasan tentang matriks banyak ditemukan dalam ilmu Matematika.
Sebagai contoh:
Diketahui jumlah penjualan mobil jenis A, B, dan C, dengan harga jual masing-masing 146, 275, dan 528 (dalam juta) pada kota-kota P, Q, R, adalah :
| JENIS MOBIL | HARGA MOBIL (JUTA) | JUMLAH PENJUALAN TIAP KOTA (UNIT) |
| KOTA P | KOTA Q | KOTA R |
| A | 146 | 34 | 56 | 41 |
| B | 275 | 45 | 36 | 37 |
| C | 528 | 51 | 32 | 46 |
Data penjualan mobil tersebut dapat dibuat dalam bentuk matriks sebagai berikut :
Matriks harga mobil adalah 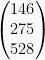
Matriks jumlah penjualan adalah 
Ordo Matriks
Dijelaskan sebelumnya matriks terdiri dari unsur-unsur yang tersusun secara baris dan kolom. Jika banyak baris suatu matriks adalah m, dan banyak kolom suatu matriks adalah n, maka matriks tersebut memiliki ordo matriks atau ukuran m x n. Perlu diingat bahwa m dan n hanya sebuah notasi, sehingga tidak boleh dilakukan sebuah perhitungan (penjumlahan, perkalian). Pada contoh matriks jumlah penjualan mobil diatas diketahui bahwa:

- Banyak baris, m = 3
- Banyak kolom, n = 3
- Ordo matriks, m x n = 3 x 3
Penamaan/notasi matriks menggunakan huruf kapital, sedangkan elemen-elemen di dalamnya dinotasikan dengan huruf kecil sesuai dengan penamaan matriks dan diberi indeks ij. Indeks tersebut menyatakan posisi elemen matriks, yaitu pada baris i dan kolom j. Sebagai contoh, matriks sebelumnya untuk penjualan mobil:
Dimana,  adalah elemen matriks yang berada pada baris ke-1 (i = 1) dan kolom ke-2 (j = 2). Begitu juga dengan elemen matriks yang lainnya.
adalah elemen matriks yang berada pada baris ke-1 (i = 1) dan kolom ke-2 (j = 2). Begitu juga dengan elemen matriks yang lainnya.
Pada matriks terdapat dua jenis diagonal, yaitu diagonal utama dan diagonal sekunder. Diagonal utama merupakan elemen-elemen dengan yang bisa membentuk garis miring. Diagonal sekunder merupakan kebalikan dari garis miring diagonal utama. Perhatikan matriks berikut:
Diagonal utama adalah elemen 34, 36, 46, sedangkan diagonal sekunder adalah elemen 41, 36, 51.
Matriks Identitas
Matriks diagonal dengan elemen-elemen diagonal utamanya bernilai 1 disebut matriks identitas. Pada umumnya matriks identitas dinotasikan dengan “I”. Contoh:
 atau
atau
 Jenis-jenis Matriks
Jenis-jenis Matriks
Matriks dapat dikelompokan ke beberapa jenis berdasarkan pada jumalah baris dan kolom serta pola elemen matriksnya sebagai berikut :
1. Matriks Baris dan Matriks Kolom
Matriks baris adalah suatu matriks yang hanya memiliki satu baris saja. Sedangkan, matriks kolom adalah suatu matriks yang hanya memiliki satu kolom saja. Contoh:
A = (1 4) atau B = (3 7 9) adalah matriks baris
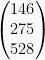 atau
atau  adalah matriks kolom
adalah matriks kolom
2. Matriks Persegi
Matriks yang memiliki jumlah kolom dan baris yang sama disebut matriks persegi. Matriks persegi memiliki ordo n.
Contoh:
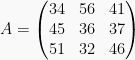 adalah matriks persegi berordo 3, atau
adalah matriks persegi berordo 3, atau
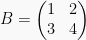 adalah matriks persegi berordo 2.
adalah matriks persegi berordo 2.
3. Matriks Segitiga Atas dan Segitiga Bawah
Matriks persegi A yang memiliki elemen matriks 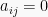 untuk
untuk  atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks
atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks 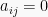 untuk
untuk 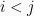 atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.
atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.
Contoh:
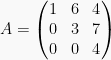 adalah matriks segitiga atas,
adalah matriks segitiga atas,
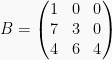 adalah matriks segitiga bawah.
adalah matriks segitiga bawah.
4. Matriks Diagonal
Matriks persegi A yang memiliki elemen matiks 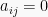 untuk
untuk  atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.
atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.
Contoh:
 atau
atau 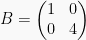
5. Matriks Skalar
Matriks diagonal yang memiliki elemen-elemen pada diagonal utamanya bernilai sama disebut matriks skalar.
Contoh:
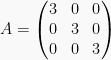 atau
atau 
6. Matriks Indentitas
sudah dijelaskan di atas
7. Matriks Simetris
Matriks persegi A yang memiliki elemen matiks baris ke-I sama dengan elemen matriks kolom ke-j untuk i = j disebut simetris. Atau, dapat dikatakan elemen 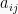 sama dengan elemen
sama dengan elemen 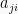 .
.
Contoh:
Dapat dilihat bahwa elemen baris ke-1 sama dengan kolom ke-1, baris ke-2 sama dengan kolom ke-2, dan baris ke-3 sama dengan kolom ke-3.
Operasi perhitungan pada matriks
Kesamaan 2 matriks :
2 matriks dikatakan sama jika ordonya sama dan elemen yang seletak sama.
Contoh: 
Tentukan nilai 2x-y+5z!
Jawab:
 maka
maka 
 maka
maka 
 maka
maka 



Penjumlahan matriks
2 matriks bisa dijumlahkan jika ordonya sama dan penjumlahan dilakukan dengan cara menjumlahkan elemen yang seletak.
Contoh: 
Pengurangan matriks
2 matriks bisa dikurangkan jika ordonya sama dan pengurangan dilakukan dengan cara mengurangkan dari elemen yang seletak.
Contoh: 
Perkalian bilangan dengan matriks
Contoh:

Perkalian matriks
2 Matriks dapat dikalikan jika jumlah baris matriks A = jumlah kolom matriks B.
Penghitungan perkalian matriks:
Misalkan:
 dan
dan 
maka 
Contoh:

Transpose Matriks
Transpose matriks merupakan perubahan baris menjadi kolom dan sebaliknya. Transpose matriks dari  adalah sebuah matriks dengan ukuran (n x m) dan bernotasi AT. Jika matriks A ditanspose, maka baris 1 menjadi kolom 1, baris 2 menjadi kolom 2, dan begitu seterusnya.
adalah sebuah matriks dengan ukuran (n x m) dan bernotasi AT. Jika matriks A ditanspose, maka baris 1 menjadi kolom 1, baris 2 menjadi kolom 2, dan begitu seterusnya.
Contoh:
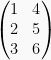 ditranspose menjadi
ditranspose menjadi  .
.
Sifat dari transpose matriks: 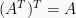 .
.
Contoh Soal dan Pembahasan
Jika 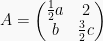 dan Jika
dan Jika 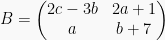 , maka agar
, maka agar 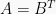 , berapakah nilai c?
, berapakah nilai c?
Pembahasan:
Diketahui bahwa 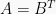
Sehingga didapat 4 persamaan baru dari elemen-elemen matriksnya, yaitu:
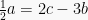 (persamaan ke-1)
(persamaan ke-1)- 2 = a (persamaan ke-2)
- b = 2a + 1 (persamaan ke-3)
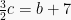 (persamaan ke-4)
(persamaan ke-4)
Dari persamaan tersebut dapat dilakukan substitusi persamaan untuk memperoleh nilai c, yaitu:
a = 2, maka:
b = 2a + 1 = 2(2) + 1 = 5
dan
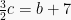
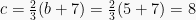 .
.
Refrensi materi diatas dan bisa anda kunjungin juga untuk cari materi lain nya.





















